James Fox, Cyber Security Operations Consultant | 28 June 2024
In part one of "Uncertain Threats" we went through several analytical strategies that a security operations analyst can use at triage to manage uncertainty during an investigation, using suspicious Entra ID sign-ins as a running example.
In part two, we'll shift focus and start to build a methodology for modelling this uncertainty.
We briefly touched on a common problem that analysts face during triage; that alert involving *anomalous* activity sacrifice actionable context to catch novel threats. This makes triaging alerts like "a user exceeded the threshold for failed sign-ins by 3.49182301 standard deviations from the mean 1.2093891" difficult to grapple with.
At the core of this problem is the lack of a demonstrated relationship between the context yielded in an alert like this, and the threat (or threats) that it is indicative of. What does "3.49182301 standard deviations" actually mean in terms of confirming or denying that a threat exists?
In an ideal world, an analyst should instead be presented with a score showing how *probable* the activity is indicative of threat (or benign) scenarios to help guide investigative effort. For example, "Password spraying by compromised user (78%)". To do this, we need to find a way to model the *uncertainty* of a threat given a wide range of potential indicators.
At the core of cybersecurity operations is alert investigation and triage. At this stage, security operations analysts decide on the disposition of an alert by collecting and analysing evidence in an investigation. These dispositions are usually expressed as either a false, benign, or true positive. In the stark majority of cases, it is not possible for an analyst to come to a single disposition with 100% confidence. There is always room for uncertainty. Often this is a by-product of uncertainty in the source of the evidence used to form the disposition - which more often than not is log data.In general, logs are not directly representative of a threat. Instead, they are a demonstration of the relationship between a threat and the monitored environment. The strength of this relationship can be thought of in terms of conditional probability, that is, the probability that a threat has caused the activity observed in the environment (i.e. the logs).
Therefore, triage at the fundamental level is simply a process of comparing probabilities. If the probability of a threat outweighs the probability of a benign or false-positive, then some action needs to be performed in response. Otherwise, more context needs to be gathered or the alert can be dismissed.
We can use Bayesian statistics as a framework for building a mathematical relationship between alert dispositions (i.e. the investigation hypotheses) and evidence. Unlike traditional statistical approaches, where probability is derived from the frequency of events, Bayesian statistics interpret probability as a measure of belief in a hypothesis. In our case, the belief that a threat exists (or not).
Personally, all this talk of statistics makes my eyes glaze over, so we'll go through some key concepts in Bayesian statistics alongside how they can be understood with reference to security operations to make things easier:-
Therefore, if we can calculate the posterior probability for each hypothesis given all of our evidence, we can calculate what the most probable disposition is by summing up and comparing the posterior probabilities for distinct threat and benign class hypotheses. For example, consider the threat hypothesis T1, and benign hypothesis B1, that we'd like to find the posterior probabilities of given the evidence E that a user has signed in from an unfamiliar location:
We can assign prior probabilities for the hypotheses based on our knowledge of past incidents, or empirical analysis:
Then, we need values for the likelihoods. We can find this again by looking at the frequency of unfamiliar travel in incidents involving the two hypotheses, or prior analyst judgement (a best guess):
We can then calculate the marginal likelihood of there being an unfamiliar sign-in location:
P(E) = P(E ∣ T1) ⋅ P(T1) + P(E ∣ B1) ⋅ P(B1) = 0.31
Finally, we can use Bayes' theorem to calculate the posterior probability of the two competing hypotheses:
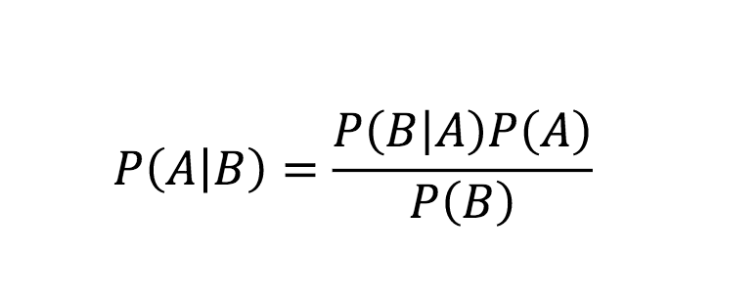
The analyst can then conclude that a sign-in involving an unfamiliar location is probably the result of legitimate travel since P(B1 | E) > P(T1 ∣ E).
But can they really?
In a real-world triage, an analyst is considering multiple competing hypotheses and many (many) different pieces of evidence. This is critical to come to high confidence and accurate dispositions on the nature of a threat. For example, if instead we considered the following pieces of evidence our conclusion on the nature of an AiTM threat would be stronger:
As you may have already noticed, sometimes evidence can confirm or refute multiple hypotheses in an investigation. In the above example, "unfamiliar sign-in location" can indicate a potential AiTM threat, but also legitimate user travel. Compounding this problem further are instances of conditional dependency between our pieces of evidence. For example, indication of an "unregistered Entra ID device" used in a sign-in flow would have a strong dependent relationship on "Unfamiliar OS user agent" since they both relate to a user signing in from an anomalous device.
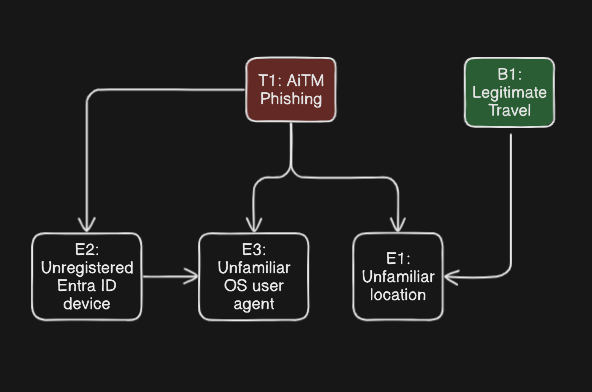
Other than the aforementioned lack of context given to analysts during triage, this is another major reason why confident dispositions can be hard to reach. With the addition of many hypotheses, and kinds of evidence, and the relationships between them all, it's challenging to accurately calculate or even estimate probability.
In our experience, this can lead to analysts arbitrarily weighting evidence that has stronger relationships to a hypothesis at the expense of all others, essentially cutting away the noise and ambiguity when forming a disposition. For example, an analyst may dismiss an alert for AiTM phishing if there was no evidence of a URL click on a suspicious email - even despite sign-in activity indicating otherwise, since a URL click on a suspicious email is a much stronger indicator of AiTM phishing than just anomalous sign-in activity.
This is problematic, but somewhat unavoidable when analysts are required to reason about large volumes of evidence and potential threats. SOC analysts triaging alerts are going to tend toward optimising their process through heuristics the more alerts of a similar kind are seen over and over (and over) again. Instead, we can seek to fix this by encoding these complex probabilistic relationships between evidence and potential hypotheses in some kind of model, that can be used at triage-time to calculate the posterior probabilities of each hypothesis...
A Bayesian Belief Network (BBN) is a graphical model that represents a set of variables (our hypotheses and evidence) and their conditional dependencies through a directed acyclic graph (DAG). BBNs are well suited to this kind of problem, since they can be used for probabilistic inference and make good use of domain knowledge through the graph's structure.
There are a few key elements of BBNs:
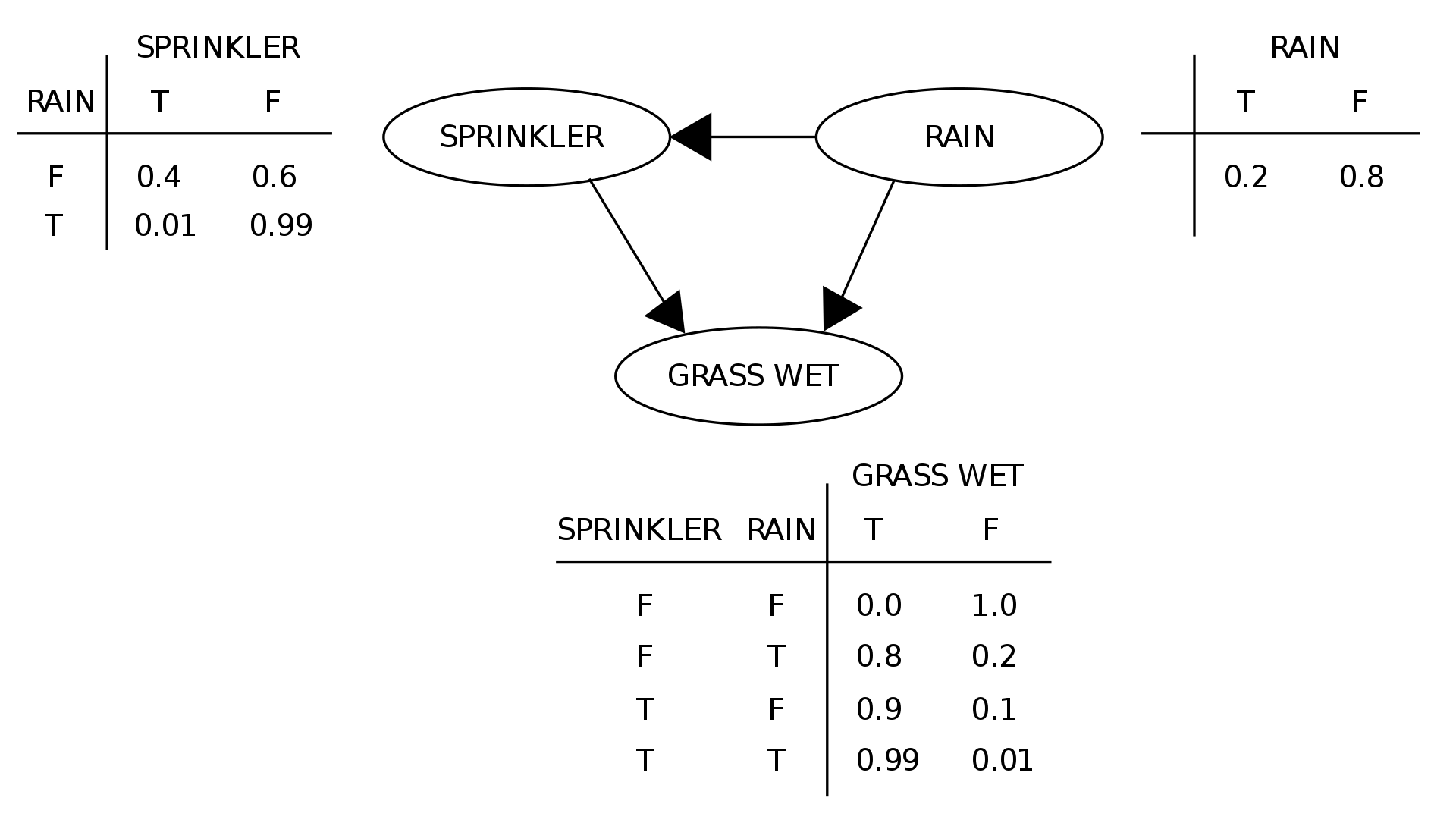
There are several benefits of using BBNs to model our problem, other than just being able to calculate posterior probabilities. The key being that BBNs are intuitively easier for a human (or analyst) to understand as opposed to massive joint probability tables. Moreover, BBNs excitingly allow for Bayesian inference for machine learning - that is, the prior probabilities can be updated over time using completed triages to improve the accuracy of the confidence estimations. For example, if we calculate the confidence of a user being compromised through a password spraying attack as 78%, and the analyst confirms this to be the case, the actual posterior probability is 100%. Therefore, we can adjust the related prior probabilities in the BBN to match this expectation.
The following process can be used to build the structure of a Bayesian Belief Network that can be used by an analyst to support inference on the likelihood of several competing hypotheses given some evidence in an investigation:
After the structure of the network is defined, we then need to assign conditional probabilities to each of the nodes (hypotheses and evidence) in the form of a conditional probability table. This is by far the trickiest part, since we need a way to find these based on past categorised activity or best-judgment (a guess).
For example, we can estimate the probability of "unfamiliar location" in the hypothesis of "AiTM phishing" by calculating the frequency of past investigated AiTM phishing incidents involving an "unfamiliar location". We can perform a similar evaluation to calculate marginal likelihoods, that is, the probability of "unfamiliar location" being in any sign-in event in the user's activity.
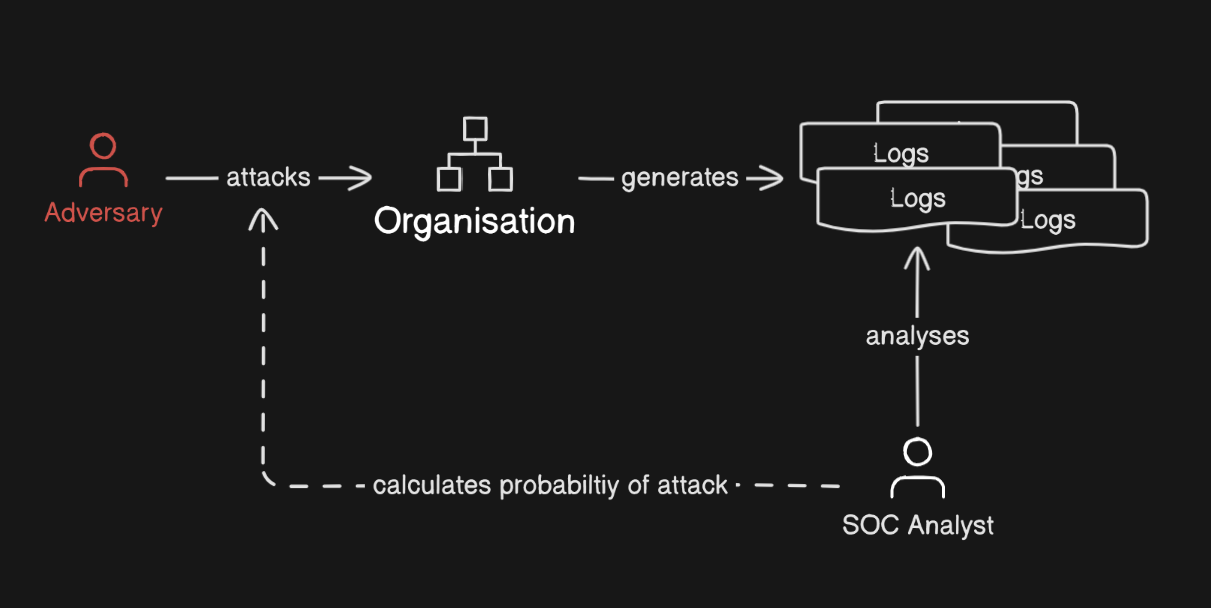
Putting it all together, we would now have a functional BBN which integrates into our typical SOC SOAR process as follows
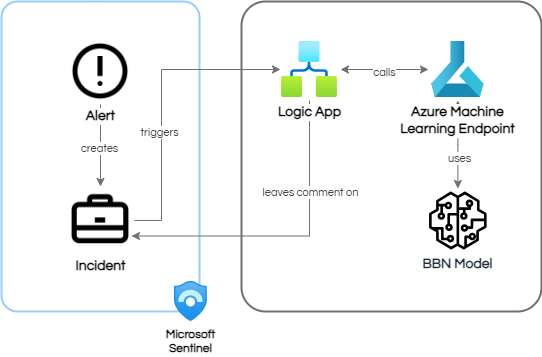
In this instalment of "Uncertain Threats", we've built a rationale as to how Bayesian Belief Networks can be used in security operations to model uncertainty, allowing for analysts to come to quantifiable decisions on the nature of an alert.
We went through some basics of Bayesian probability and used it as a foundation for explaining the inherit complexity of triage in security operations. Finally, an example workflow was given for how the structure of BBN can be purpose-built, then integrated into a real-world triage process to directly support analysts.
In part three of the series, we'll build an operational Bayesian Belief Network for automated inference on the nature of threats against Microsoft Entra ID - including a sample model, joint probability tables, queries, and code.
Stay tuned!
Request a consultation with one of our security specialists today or sign up to receive our monthly newsletter via email.
Get in touch Sign up!